Bekenstein Bound

In physics, the Bekenstein bound (named after Jacob Bekenstein) is an upper limit on the thermodynamic entropy ''S'', or Shannon entropy ''H'', that can be contained within a given finite region of space which has a finite amount of energy—or conversely, the maximal amount of information required to perfectly describe a given physical system down to the quantum level. It implies that the information of a physical system, or the information necessary to perfectly describe that system, must be finite if the region of space and the energy are finite. In computer science this implies that non-finite models such as Turing machines are not realizable as finite devices.

Equations

The universal form of the bound was originally found by Jacob Bekenstein in 1981 as the inequality

: $S \leq \frac,$

where ''S'' is the entropy, ''k'' is the Boltzmann constant, ''R'' is the radius of a sphere that can enclose the given system, ''E'' is the total mass–energy including any rest masses, ''ħ'' is the reduced Planck constant, and ''c'' is the speed of light. Note that while gravity plays a significant role in its enforcement, the expression for the bound does not contain the gravitational constant ''G'', and so, it ought to apply to quantum field theory in curved spacetime.

In informational terms, the relation between thermodynamic entropy ''S'' and Shannon entropy ''H'' is given by

: $S = kH\ln 2,$

whence

: $H \leq \frac,$

where ''H'' is the Shannon entropy expressed in number of bits contained in the quantum states in the sphere. The ln 2 factor comes from defining the information as the logarithm to the base 2 of the number of quantum states. Using mass–energy equivalence, the informational limit may be reformulated as

:$H \leq \frac \approx 2.5769082 \times 10^\ \frac \cdot M\cdot R,$

where $M$ is the mass (in kg), and $R$ is the radius (in meter) of the system.

Origins

Bekenstein derived the bound from heuristic arguments involving black holes. If a system exists that violates the bound, i.e., by having too much entropy, Bekenstein argued that it would be possible to violate the second law of thermodynamics by lowering it into a black hole. In 1995, Ted Jacobson demonstrated that the Einstein field equations (i.e., general relativity) can be derived by assuming that the Bekenstein bound and the laws of thermodynamics are true.Lee Smolin, '' Three Roads to Quantum Gravity'' (New York, N.Y.: Basic Books, 2002), pp. 173 and 175, , . However, while a number of arguments were devised which show that some form of the bound must exist in order for the laws of thermodynamics and general relativity to be mutually consistent, the precise formulation of the bound was a matter of debate until Casini's work in 2008. Jacob D. Bekenstein
"Information in the Holographic Universe: Theoretical results about black holes suggest that the universe could be like a gigantic hologram"
''Scientific American'', Vol. 289, No. 2 (August 2003), pp. 58-65
Mirror link
. Tipler gives a number of arguments for maintaining that Bekenstein's original formulation of the bound is the correct form. See in particular the paragraph beginning with "A few points ..." on p. 903 of the ''Rep. Prog. Phys.'' paper (or p. 9 of the ''arXiv'' version), and the discussions on the Bekenstein bound that follow throughout the paper.

Suppose we have a black hole of mass $M$ and a box of energy $E$ outside it of size $R$. The radius of the black hole, $R_$ goes as $\frac$ and the entropy of the black hole goes as $\frac$ which goes as $\frac$. If we dump the box into the black hole, the mass of the black hole goes up to $M+\frac$, and the entropy goes up by $\frac$ . Since entropy can't decrease, $\frac\gtrsim S$ . In order for the box to fit inside the black hole, $R \lesssim \frac$ . If the sizes are comparable, then $S \lesssim \frac$. Working out the actual coefficients requires a more technical analysis.

Proof in quantum field theory

A proof of the Bekenstein bound in the framework of quantum field theory was given in 2008 by Casini. One of the crucial insights of the proof was to find a proper interpretation of the quantities appearing on both sides of the bound.

Naive definitions of entropy and energy density in Quantum Field Theory suffer from ultraviolet divergences. In the case of the Bekenstein bound, ultraviolet divergences can be avoided by taking differences between quantities computed in an excited state and the same quantities computed in the vacuum state. For example, given a spatial region $V$, Casini defines the entropy on the left-hand side of the Bekenstein bound as

: $S_V = S(\rho_V) - S(\rho^0_V) = - \mathrm(\rho_V \log \rho_V) + \mathrm(\rho_V^0 \log \rho_V^0)$

where $S(\rho_V)$ is the Von Neumann entropy of the reduced density matrix $\rho_V$ associated with $V$ in the excited state $\rho$, and $S(\rho^0_V)$ is the corresponding Von Neumann entropy for the vacuum state $\rho^0$.

On the right-hand side of the Bekenstein bound, a difficult point is to give a rigorous interpretation of the quantity $2\pi R E$, where $R$ is a characteristic length scale of the system and $E$ is a characteristic energy. This product has the same units as the generator of a Lorentz boost, and the natural analog of a boost in this situation is the modular Hamiltonian of the vacuum state $K=-\log \rho_V^0$. Casini defines the right-hand side of the Bekenstein bound as the difference between the expectation value of the modular Hamiltonian in the excited state and the vacuum state,

: $K_V = \mathrm(K \rho_V) - \mathrm(K \rho^0_V).$

With these definitions, the bound reads

: $S_V \leq K_V,$

which can be rearranged to give

: $\mathrm(\rho_V \log \rho_V) - \mathrm(\rho_V \log \rho_V^0) \geq 0.$

This is simply the statement of positivity of quantum relative entropy, which proves the Bekenstein bound.

However, the modular Hamiltonian can only be interpreted as a weighted form of energy for conformal field theories, and when V is a sphere.

This construction allows us to make sense of the Casimir effect where the localized energy density is ''lower'' than that of the vacuum, i.e. a ''negative'' localized energy. The localized entropy of the vacuum is nonzero, and so, the Casimir effect is possible for states with a lower localized entropy than that of the vacuum. Hawking radiation can be explained by dumping localized negative energy into a black hole.

Examples

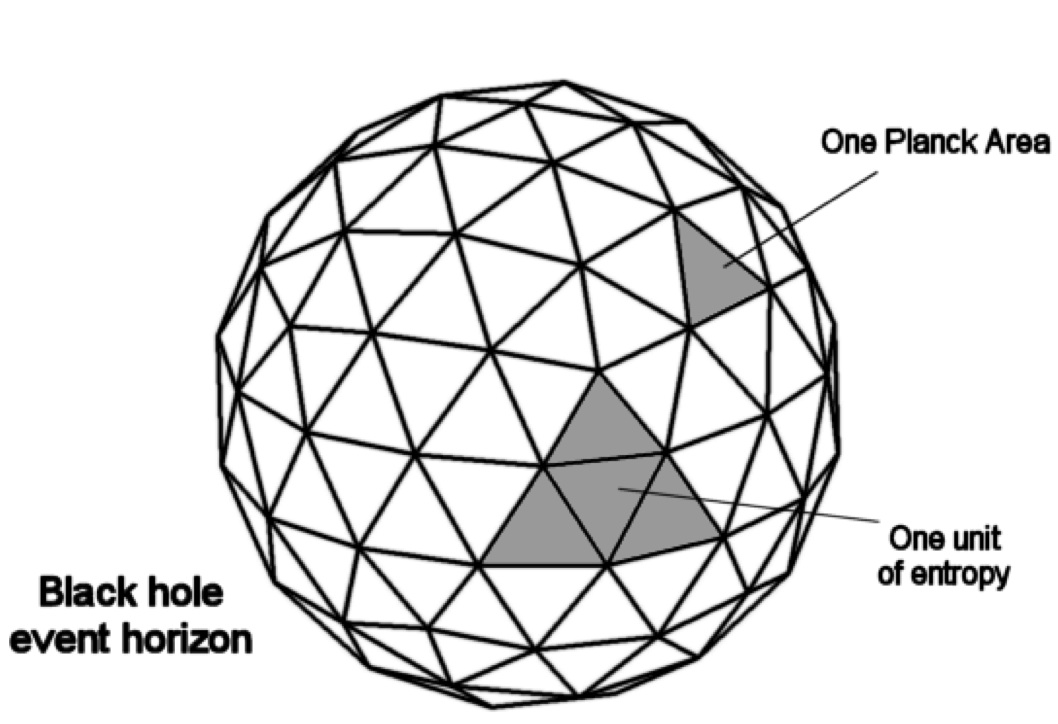
Black holes

It happens that the Bekenstein–Hawking boundary entropy of three-dimensional black holes exactly saturates the bound

: $r_ = \frac,$
: $A = 4 \pi r_^2 = \frac,$
: $l_^2 = \hbar G/c^3,$
: $S = \frac = \frac,$

where $k$ is the Boltzmann constant, ''A'' is the two-dimensional area of the black hole's event horizon and $l_$ is the Planck length.

The bound is closely associated with black hole thermodynamics, the holographic principle and the covariant entropy bound of quantum gravity, and can be derived from a conjectured strong form of the latter.

Human brain

An average human brain has a mass of 1.5 kg and a volume of 1260 cm. If the brain is approximated by a sphere, then the radius will be 6.7 cm.

The informational Bekenstein bound will be about 2.6 bits and represents the maximal information needed to perfectly recreate an average human brain down to the quantum level. This means that the number $O = 2^I$ of states of the human brain must be less than $\approx 10^$.

See also

* Margolus–Levitin theorem
* Landauer's principle
* Bremermann's limit
* Kolmogorov complexity
* Beyond black holes
* Digital physics
* Limits to computation
* Chandrasekhar limit

References

External links

* Jacob D. Bekenstein
"Bekenstein bound"
''Scholarpedia'', Vol. 3, No. 10 (2008), p. 7374, .
* Jacob D. Bekenstein
"Bekenstein-Hawking entropy"
''Scholarpedia'', Vol. 3, No. 10 (2008), p. 7375, .

Jacob D. Bekenstein's website
at the Racah Institute of Physics, Hebrew University of Jerusalem, which contains a number of articles on the Bekenstein bound.
*

Limits of computation
Thermodynamic entropy
Quantum information science
Black holes

{{Quantum gravity